【看中國2022年4月1日訊】1956年,物理學家約翰-凱利(John Larry Kelly),在《貝爾技術期刊》上,發了一篇題為「信息比例新解(A New Interpretation Of Information Rate)」的論文。

物理學家約翰-凱利(John Larry Kelly。作者博客)
在這篇論文中,凱利提出了一個如何處理信息傳輸中信號和噪音的公式,這就是後來大名鼎鼎的「凱利公式(Kelly Formula)」:
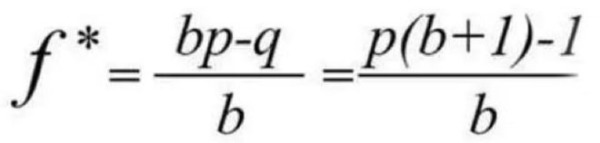
其中:f為信號發射端每次發送信號佔總信息量的比率;p為接收端接收到有效信號佔總信息量的比率;q為接收端接收到噪音信號佔總信息量的比率,q=1-p;b為特定介質在信息傳輸過程中的信噪比(信號與雜訊的比值)。
這篇論文,看上去科學嚴謹又高大上,但實際上完全不是那麼回事兒——因為,這個公式是凱利在研究一個賭博遊戲時琢磨出來的。
當時有一檔電視答題節目正在熱播,名叫《64000美元的問題》,因為節目火爆,就有人賭哪位選手能獲勝。賭徒們能夠提前獲取一部分選手的信息,但這些信息有限而且可能有誤,賭徒需要在不完全信息下進行下注。
凱利瞭解到這個賭局之後,就開始琢磨,如何利用有限的信息來參與賭博,才能在保證永遠不輸完的情況下,實現「利潤最大化」?
經過反覆的推導,凱利總結出來了如下公式:
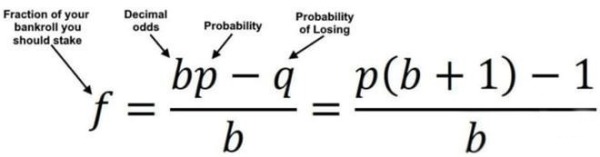
凱利公式的投資意義(作者博客)
其中的f,為計算出來的賭金最優投資比例,b為賠率,即期望盈利/預計虧損,p為成功概率,q為失敗概率即1-p。
舉個例子,假設一個拋硬幣猜正反的簡單賭局,每局賭注1元,猜中了得2元,猜錯了輸掉1元,也就是賠率b=2,勝率p=0.5,代入公式後算得f=0.25——也就是說,在這樣一個簡單拋硬幣賭局中,如果能夠無限次重複,每次投入所持有本金的25%,可以在永遠不輸光本金的前提下實現收益的最大化。
從這個公式裡可以得出來兩個推論:
1)除非勝率是100%,否則任何賭局都不能all in;
2)f為正值的賭局才值得參與,f為0或負值的遊戲,重複參與的人必輸無疑。
別人的一個賭博遊戲,凱利能總結出如此簡潔的數學公式,由此可見凱利之聰明。凱利此人不僅長得帥,聰明,還特別有趣。在加入貝爾實驗室之前,他是美國海軍的飛行員,加入貝爾實驗室之後,他還加入了槍械俱樂部,又和妻子組隊打橋牌錦標賽,還給敞篷車裝上彈射座椅……
不過,在當時的貝爾實驗室:
凱利的帥,只能排第二位;
凱利的聰明,也只能排第二位;
凱利的有趣好玩,還是只能排第二位。
以上三項,都穩排在第一位的那個傢伙,叫香農(Claude Elwood Shannon)。

貝爾實驗室的克勞德-香農(作者博客)
很多人可能沒聽說過這個人。但其實,香農是當代資訊理論的開山鼻祖。他的碩士論文以及後來發表在《貝爾技術期刊》上的兩篇論文,確立了當代通信編碼的基本原理,他用數學公式來描述通信定理,為資訊理論和數字通信奠定了基礎。正是沿著他的思路,才有了今天的網際網路世界。
某種程度上說,現在的我們,能夠在網際網路上自由地即時聊天、打電話、聽音樂、看電影等等,其實都應該感謝他。
話說凱利總結出這個公式後,就拿給香農看,香農建議他寫成文章。起初,題目是「信息理論與賭博」,但貝爾實驗室的東家AT&T擔心,大眾可能認為實驗室在拿著研究資金搞非法賭博,所以在發表時名字特意改成了「信息比新解」。
凱利公式發表後,一直沒有激起什麼特別的浪花,直到被一個叫愛德華-索普(Edward O.Thorp)的傢伙給看到。
索普這人,從小就是個數學計算神童,28歲就在著名的麻省理工學院當了數學講師。但他從小就喜歡研究賭博,一直想要找到一種方式,通過大量的數據計算,來預測輪盤賭中彈珠最後的大致位置。
1960年,索普大致完成了自己的猜想,他想將論文發表在美國科學院院刊上,但這個刊物規定,必須由科學院院士推薦或署名才行。於是,索普就找到了當時麻省理工唯一的國家科學院院士——香農。
香農一直都是個老頑童,索普的這種主意很快就打動了他,他同意推薦論文發表,然後,按照索普的理論,兩個人一起製造了一個簡易的計算器,到各個輪盤賭上去小試身手。結果發現,因為各種計算誤差,賭博成果一直都差強人意。
這個時候,香農忽然想起來凱利公式,就把這篇論文,推薦給了索普,索普一眼就看了出來,這個公式可以應用到當時各大賭場盛行的21點賭博遊戲中——該遊戲由2到6個人玩,使用除大小王之外的52張撲克牌,遊戲者的目標,是使手中的牌的點數之和不超過21點且盡量大。
為了驗證凱利公式和「數牌法」在實際中的效果,索普於是約了一個專業賭徒,拿著1萬美元的本錢,到附近的兩個小賭場裡小試身手,結果,僅一個週末裡,就狂賺1.1萬美元。
確認策略有效後,索普聯合香農,設計了史上第一個攜帶型「計算器」。接下來,一旦沒錢花了或者手痒難耐的時候,索普就和香農及夫人在週末坐上飛機,飛往拉斯維加斯,在賭場裡大玩21點,掙一大把錢後走人。

投資達人愛德華-索普(作者博客)
由於索普在賭場中屢屢獲勝,不久就被各大賭場列為「不受歡迎的人」。為了能繼續贏下去,索普使用了化妝術,後來乾脆雇佣別人代替他本人去賭博,但賭場也越來越警惕。
索普的名聲在賭博業裡傳開了,很多人都想學這種方法。索普乾脆從挖金子改行賣鏟子,於是在1962年寫了一本書:《戰勝莊家:21點中的獲勝策略》(Beatthe Dealer: A Winning Strategy for the Game of Twenty-One),詳細披露了自己是如何在賭場中賺錢的。
這本書迅速登上紐約時報暢銷書排行榜,銷量高達70萬冊,比索普本人化妝去辛苦賭博掙錢多多了,這也證明了一個真理:賣鏟子比挖金子賺錢。
那我們來看看,索普到底是怎麼在21點的賭博中掙錢的呢?
其實很簡單,記牌!
因為21點是撲克牌遊戲,而每一副牌中某花色或點數的總量是一定的,每一輪賭博過後,發牌員手中的牌數就會減少。通過記下已經出現的牌,索普就能計算髮牌員手中有什麼樣的牌,然後根據這些牌的花色、點數估算出現不同情況的概率,進而用凱利公式來計算下注比例。形勢有利的時候就下大賭注,形勢不利的時候就下小賭注。
那個時代賭場也很「笨」,一般只用1-2副牌,而且發牌員常常將牌發完之後才洗牌,導致記牌並非難事。索普公布了自己的辦法之後,賭場就學精了,每次用6-8副牌,而且發牌不到1/3就重新洗牌,而且禁止攜帶電腦和數牌的電子設備進場,基本就堵上了這個漏洞。
索普的書暢銷了之後,凱利公式開始變得世人皆知,甚至有人稱之為「財富公式」。
到了1969年,一個年輕的紐約證券經紀人里根找到了索普,希望和索普一起成立一個對沖基金,將索普的理念和方法完全商業化。索普可以繼續做他的研究,並作為基金經理下交易指令,而里根幫助他做產品銷售,客戶維護,完成交易執行以及其他所有的瑣事。
從1969年成立,到1988年因訴訟而意外停業,索普的基金20年年化收益率19.1%。雖然在投資大師裡貌似不算驚人,但如果你查看該基金淨值會發現,近20年的跨度下,該基金居然沒有一年虧損,共計230個月,只有3個月有回撤,且回撤幅度全部小於1%——這,大概是有史以來「最完美的投資曲線」。
實際上,索普的基金,是美國第一隻完全的中性策略基金,僅基於數學計算的概率和市場的定價失誤進行投資,即使在1987年的美股暴跌中,索普的基金也基本保持穩定,到年末,甚至還賺了大錢。
隨著參與到華爾街的「大賭博」中來,索普見了許多投資界人士,其中有一個叫巴菲特。那個時候他還不是股神,但兩人交流之後惺惺相惜,索普甚至預言,巴菲特會成為美國最富有的人。多年之後的巴菲特,的確實現了索普的預言。
索普認為,巴菲特是真正的投資大師,所以他把自己相當一部分財富,入股了巴菲特的公司,成為巴菲特的早期股東之一,這些股份一直持有到現在。
1994年,索普重新成立了一家對沖基金,這個基金業績更好,可惜到2002年他也主動解散——外部原因來說,是對沖基金數量激增,交易機會減少,但更重要的原因,是索普對賺錢的興趣降低了,他覺得和家人在一起,才是更好的時光。
索普對名聲也並不在意,後來震動了整個投資界Black-Scholes期權定價模型,其實索普自己早已推導出來,但他的選擇是自己默默掙錢。後來,這個公式的兩位作者布萊克(Black)和斯科爾斯(Scholes),還特意在論文裡感謝索普的貢獻。
索普對此很平靜:「我從未考慮過我的榮譽,因為我不是從事經濟學和金融行業研究的人,這個問題附帶的重大意義並不在我的思考範圍。」
相比於索普研究的個人化和隱私化,BS期權定價模型讓每個投資者都可以預測期權價格,它的提出徹底顛覆了以往的金融運行體系,華爾街的量化投資時代正式到來了。到了後來,麻省理工教授羅伯特-默頓(Robert Merton)採用隨機微積分將公式進一步完善,他和斯科爾斯共同獲得了1997年的諾貝爾經濟學獎。
所以,某種程度上說,索普是當今所有量化投資的鼻祖。
實際上,當前金融市場上叱吒風雲的知名對沖基金經理,幾乎都在使用凱利公式進行投資,這其中包括比爾-格羅斯(Bill Gross,債券投資之王)、詹姆斯-西蒙斯(James Simons,文藝復興公司名譽主席、世界級的數學家)和投機之王喬治-索羅斯(George Soros)等人。
特別值得一提的是,索普不再做對沖基金後,偶爾會做一些基金管理諮詢的事情,結果他就發現,伯納德-麥道夫的證券投資公司大有問題,勸朋友把錢撤出來。果不其然,2008年的時候,這一美國歷史上最大的「龐氏騙局」被揭露,詐騙金額超過600億美元。
索普寫了一本自傳《A Man For All Markets》,這裡的All Markets,意思是,他涉及了幾乎所有的交易市場,從賭場到華爾街,OTC期權、可轉債、股票、期貨等……
另外,如今在美國量化對沖基金領域鼎鼎大名的TGS基金,據說就是索普的三個徒弟一起創辦的,而TGS中的「T」,就是Thorp的名字。
看完那這篇文章覺得























排序