加薪靠實力？為何薪資差距越來越大(組圖)

加薪靠實力？為何薪資差距越來越大。（圖片來源：Adobestock）

加薪靠的是實力？三分鐘瞭解為什麼薪資差距越來越大  

編按：常見的加薪方式不外乎是多發放一筆定額獎金，或是額外發放薪資的一定比例，這兩種加薪方式何者比較公平？又會形成什麼樣的結果？

以下為《多模型思維》作者裴吉應用數學模型研究「加薪」的討論：

對數常態分佈：衝擊相乘

若利用中央極限定理，則需要將獨立的隨機變數加總或平均，來得到常態分佈。如果隨機變數使用加法以外的方式互動，或者並非獨立，產生的分佈就不一定是常態分佈了，或者說，幾乎都不是常態分佈。

例如：獨立隨機變數相乘產生的隨機變數為「對數常態分佈」，而非常態分佈。大於1的數字相乘，放大效果比相加還要明顯，例如4 ＋ 4 ＋ 4 ＋ 4 ＝16，但4 × 4 × 4 × 4 ＝ 256。小於1 的數字相乘，縮小效果又會比相加還要明顯，例如1/4 ＋ 1/4 ＋ 1/4 ＋ 1/4 ＝ 1，但1/4 × 1/4 × 1/4 × 1/4 ＝ 1/256。

因此，對數常態分佈並非對稱圖形。如果有多組均勻分佈在0 到10 之間的二十個隨機變數，相乘之後會包含許多接近零的結果與部分超大數值，形成下圖中的偏態分佈（skewed distribution）。

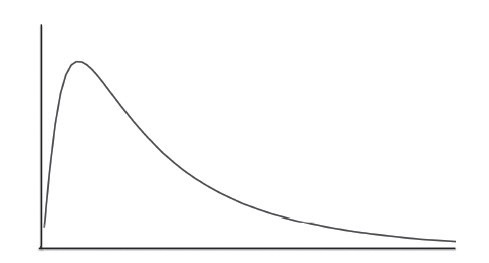
（圖片來源：天下文化）

對數常態分佈的長尾，長度取決於隨機變數的變異數相乘結果。如果變異數很小，尾巴就會很短；如果變異數很大，尾巴就會非常長。理由就如同上一段提到的，一系列大數值相乘，會產生非常巨大的數值。

對數常態分佈的例子很多，包含英國農莊大小、地球礦物集中度，以及從感染疾病到出現症狀的時間。 許多國家的收入分佈也很接近對數常態分佈，但是很多國家的長尾端有太多高收入人群，導致偏離了對數常態分佈。

利用簡單的模型，將加薪政策與隱含收入分佈進行連結，就能解釋為什麼收入分佈更接近對數常態分佈，而非常態分佈。例如，大多數的企業組織以百分比方式計算加薪，表現優於平均的員工得到高百分比加薪，表現低於平均的員工得到低百分比加薪。

企業組織當然也可以採用絕對金額方式加薪──表現在平均值的員工可以獲得加薪一千美元，表現好則得到更高加薪，表現差得到更少加薪。百分比和絕對金額加薪，看起來只是換湯不換藥，其實兩者有顯著差異。

如果員工每年的表現是獨立且隨機，且依照員工表現以百分比加薪，就會產生對數常態分佈收入。就算兩名員工的表現每年都相同，隨著年度增加，起始薪資不同造成的收入差距，就會愈來愈大。

例如，年薪八萬美元、表現良好的員工，在5% 下會獲得加薪四千美元；但是年薪六萬美元的員工，在同樣5% 下，卻只能獲得加薪三千美元。因此，就算表現相同，起跑點不同也會讓薪資差距擴大。

如果公司是按照絕對金額來加薪，兩位表現相同的員工會得到同額加薪，收入分佈將接近常態分佈。
 

本文整理、節錄自 裴吉Scott E. Page《多模型思維－天才的32個思考策略》一書，文章僅代表作者個人立場和觀點。由天下文化授權轉載，欲閱讀完整作品，歡迎參考原書。